* "파이썬 머신러닝 완벽 가이드" 서적, 여러 개인 블로그들을 참고한 개인 공부용입니다
군집평가
- 비지도학습의 특성상 어떠한 지표라도 정확하게 성능을 평가하기 어렵다
실루엣 분석
다른 군집간은 비슷한 정도의 여유 거리가 있고, 동일 군집 데이터끼리는 가까운지 분석
- 실루엣 계수를 기반으로 하며 실루엣 계수는 개별 데이터가 가지는 군집화 지표이다.
실루엣 계수는 다음과 같이 표현할 수 있다.
s(i) = (b(i)−a(i)) / max(a(i),b(i))
- a(i): i번째 데이터에서 자신이 속한 군집내의 다른 데이터까지의 거리들의 평균
- b(i): i번째 데이터에서 가장 가까운 타 군집내의 다른 데이터까지의 거리들의 평균
- b(i)−a(i) : 두 군집 간 거리가 얼마나 떨어져 있는가
- / max(a(i),b(i)) : 정규화
실루엣 계수는 -1 ~ 1 사이 값을 가지며 1에 가까울수록 근처 군집과 멀리 떨어져 있다는 의미이다.
0에 가까울수록 근처 군집과 가까워지며, 음수값은 i 번째 데이터가 아예 다른 군집에 할당되었다는 의미이다.
<좋은 군집화가 되려면?>
- 전체 실루엣 계수의 평균값, (silhouette_score()) : 0~ 1 사이의 값, 1에 가까울수록 좋다.
- 전체 실루엣 계수의 평균값과 더불어 개별 군집의 편균값의 편차가 크지 않아야 함. 개별 군집의 실루엣 계수 평균값이 전체 실루엣 계수의 평균값에서 크게 벗어나지 않아야함.
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
# iris 데이터
iris = load_iris()
feature_names = ['sepal_length','sepal_width','petal_length','petal_width']
iris_df = pd.DataFrame(data=iris.data, columns=feature_names)
# KMeans
kmeans = KMeans(n_clusters=3, init="k-means++", max_iter=300, random_state=0)
kmeans.fit(iris_df)
# 데이터 프레임에 cluster 추가
iris_df["cluster"] = kmeans.labels_
# 개별 데이터 실루엣 계수
score_samples = silhouette_samples(iris.data, iris_df.cluster)
print(f'silhouette_samples( ) return 값의 shape: {score_samples.shape}')
# 데이터 프레임에 실루엣 계수 추가
iris_df['silhouette_coeff'] = score_samples
# 모든 데이터의 평균 실루엣 계수
average_score = silhouette_score(iris.data, iris_df.cluster)
print(f'붓꽃 데이터셋 Silhouette Analysis Score: {average_score:.3f}')
iris_df.groupby('cluster')['silhouette_coeff'].mean()silhouette_samples( ) return 값의 shape: (150,)
붓꽃 데이터셋 Silhouette Analysis Score: 0.553
cluster
0 0.417320
1 0.798140
2 0.451105
Name: silhouette_coeff, dtype: float64
- 평균 실루엣 계수 값 : 0.553
- "1" 군집의 경우 개별 군집 실루엣 계수가 유난히 크고, 나머지 군집 실루엣 계수 평균값은 낮다. => 좋은 군집화 조건이 아님.
군집별 평균 실루엣 계수의 시각화를 통한 군집 개수 최적화 방법
def visualize_silhouette_sklearn(range_n_clusters, X):
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
for n_clusters in range_n_clusters:
# Create a subplot with 1 row and 2 columns
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)
# The 1st subplot is the silhouette plot
# The silhouette coefficient can range from -1, 1 but in this example all
# lie within [-0.1, 1]
ax1.set_xlim([-0.1, 1])
# The (n_clusters+1)*10 is for inserting blank space between silhouette
# plots of individual clusters, to demarcate them clearly.
ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])
# Initialize the clusterer with n_clusters value and a random generator
# seed of 10 for reproducibility.
clusterer = KMeans(n_clusters=n_clusters, random_state=10)
cluster_labels = clusterer.fit_predict(X)
# The silhouette_score gives the average value for all the samples.
# This gives a perspective into the density and separation of the formed
# clusters
silhouette_avg = silhouette_score(X, cluster_labels)
# Compute the silhouette scores for each sample
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 10
for i in range(n_clusters):
# Aggregate the silhouette scores for samples belonging to
# cluster i, and sort them
ith_cluster_silhouette_values = \
sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
# Label the silhouette plots with their cluster numbers at the middle
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
# Compute the new y_lower for next plot
y_lower = y_upper + 10 # 10 for the 0 samples
ax1.set_title('Number of Cluster : '+ str(n_clusters)+'\n' \
'Silhouette Score :' + str(round(silhouette_avg,3)))
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
# The vertical line for average silhouette score of all the values
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
ax1.set_yticks([]) # Clear the yaxis labels / ticks
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
# 2nd Plot showing the actual clusters formed
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(X[:, 0], X[:, 1], marker='.', s=30, lw=0, alpha=0.7,
c=colors, edgecolor='k')
# Labeling the clusters
centers = clusterer.cluster_centers_
# Draw white circles at cluster centers
ax2.scatter(centers[:, 0], centers[:, 1], marker='o',
c="white", alpha=1, s=200, edgecolor='k')
for i, c in enumerate(centers):
ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1,
s=50, edgecolor='k')
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
plt.show()# 가상데이터: 피처 2개, 클러스터 4개
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=500, n_features=2, centers=4, cluster_std=1,
center_box=(-10.0, 10.0), shuffle=True, random_state=1)
# K-Means K: 2
visualize_silhouette_sklearn([2], X)
- 왼쪽 그림의 x축은 실루엣 계수를 의미하며 y축은 개별 데이터 포인트로 Cluster를 구분해두었다.
- 빨간 점선(0.705)은 전체 데이터의 실루엣 계수 평균이다.
- K를 2로 설정하였을 때 전체 실루엣 계수 평균은 0.705로 높지만 Cluster 0의 실루엣 계수는 대부분 평균에 못 미친다.
- 오른쪽 그림을 보면 Cluster 0은 내부 데이터끼리 거리가 멀리 있음을 알 수 있다. => 좋은 군집화 아님
# K-Means K: 4
visualize_silhouette_sklearn([4], X)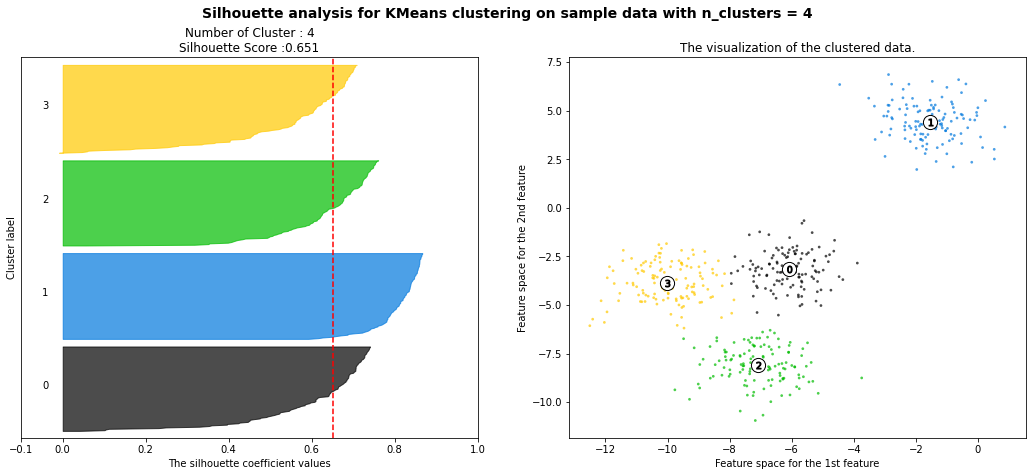
- K를 4로 설정하였을 떄 전체 실루엣 계수 평균은 0.651이고, Cluster별로 실루엣 계수가 비교적 균일하다.
- K가 2인 경우보다 전체 실루엣 계수 평균이 작지만 이상적
### 여러개의 클러스터링 갯수를 List로 입력 받아 각각의 실루엣 계수를 면적으로 시각화한 함수 작성
def visualize_silhouette(cluster_lists, X_features):
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import math
# 입력값으로 클러스터링 갯수들을 리스트로 받아서, 각 갯수별로 클러스터링을 적용하고 실루엣 개수를 구함
n_cols = len(cluster_lists)
# plt.subplots()으로 리스트에 기재된 클러스터링 수만큼의 sub figures를 가지는 axs 생성
fig, axs = plt.subplots(figsize=(4*n_cols, 4), nrows=1, ncols=n_cols)
# 리스트에 기재된 클러스터링 갯수들을 차례로 iteration 수행하면서 실루엣 개수 시각화
for ind, n_cluster in enumerate(cluster_lists):
# KMeans 클러스터링 수행하고, 실루엣 스코어와 개별 데이터의 실루엣 값 계산.
clusterer = KMeans(n_clusters = n_cluster, max_iter=500, random_state=0)
cluster_labels = clusterer.fit_predict(X_features)
sil_avg = silhouette_score(X_features, cluster_labels)
sil_values = silhouette_samples(X_features, cluster_labels)
y_lower = 10
axs[ind].set_title('Number of Cluster : '+ str(n_cluster)+'\n' \
'Silhouette Score :' + str(round(sil_avg,3)) )
axs[ind].set_xlabel("The silhouette coefficient values")
axs[ind].set_ylabel("Cluster label")
axs[ind].set_xlim([-0.1, 1])
axs[ind].set_ylim([0, len(X_features) + (n_cluster + 1) * 10])
axs[ind].set_yticks([]) # Clear the yaxis labels / ticks
axs[ind].set_xticks([0, 0.2, 0.4, 0.6, 0.8, 1])
# 클러스터링 갯수별로 fill_betweenx( )형태의 막대 그래프 표현.
for i in range(n_cluster):
ith_cluster_sil_values = sil_values[cluster_labels==i]
ith_cluster_sil_values.sort()
size_cluster_i = ith_cluster_sil_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_cluster)
axs[ind].fill_betweenx(np.arange(y_lower, y_upper), 0, ith_cluster_sil_values, \
facecolor=color, edgecolor=color, alpha=0.7)
axs[ind].text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
axs[ind].axvline(x=sil_avg, color="red", linestyle="--")
# iris 군집 개수 최적화
visualize_silhouette([ 2, 3, 4, 5 ], iris.data)
- 군집 수 2일 때, 전체 실루엣 계수 평균이 가장 높고, 각 군집별 실루엣 계수 평균도 비교적 균일하다.
'머신러닝' 카테고리의 다른 글
| [군집화] #6. DBSCAN (0) | 2022.07.19 |
|---|---|
| [군집화] #5. GMM (0) | 2022.07.19 |
| [군집화] #4. 평균이동 (0) | 2022.07.19 |
| [군집화] #2. 군집 시각화 (PCA, 군집 가상데이터 생성, K-means) (1) | 2022.07.15 |
| [군집화] #1. K-means 알고리즘 (0) | 2022.03.22 |